janmr blog

The greatest common divisor of two integers is the largest positive integer that divides them both. This article considers two algorithms for computing $\text{gcd}(u,v)$, the greatest common divisor of $u$ and $v$.

Some key properties of $\text{gcd}$ are:

1. $\text{gcd}(u,0) = |u|$.
2. $\text{gcd}(u,v) = \text{gcd}(-u,v)$.
3. $\text{gcd}(u,v) = \text{gcd}(v,u)$.
4. $\text{gcd}(u,v) = \text{gcd}(u,v+n u)$ for any integer $n$.
5. $\text{gcd}(u,v) = d \cdot \text{gcd}(u/d,v/d)$ if $d$ divides both $u$ and $v$.
6. $\text{gcd}(u,v) = \text{gcd}(u/d,v)$ if $d$ is prime and divides $u$ but not $v$.

Property 1 with $u=0$ takes care of the special case $u=v=0$. In what follows we assume that $u$ and $v$ are not both zero.

One way to define $\text{gcd}(u,v)$ is the following. Consider the set of all positive integers that divide both $u$ and $v$. This set is not empty since it always contains 1. It is also bounded since no divisor exceeds $|u|$ or $|v|$. Therefore, this set contains a maximum element, which is equal to $\text{gcd}(u,v)$. From this definition Properties 1, 2, and 3 follow easily. For the sake of simplicity, easily justified by Property 2 and 3, we will only consider non-negative $u$ and $v$.

Consider now Property 4. We prove this by showing that the set of divisors of $u$ and $v$ is equal to the set of divisors of $u$ and $v+n u$ (and hence, their gcd's must be equal). Consider then a positive integer $d$ that divides $u$ and $v$. Obviously, $d$ also divides $v+n u$. Assume now that some $d$ divides $u$ and $r=v+n u$. Then $d$ also divides $r-n u=v$.

Another useful way to define $\text{gcd}(u,v)$ is possible for positive $u$ and $v$. According to the fundamental theorem of arithmetic we can write

$$u = \prod_{p \; \rm prime} p^{u_p},$$

and similarly for $v$. We now have

$$\text{gcd}(u,v) = \prod_{p \; \rm prime} p^{\min(u_p,v_p)}.$$

Properties 5 and 6 follow from this equality.

Euclid's Algorithm

Euclid's algorithm appeared in Euclid‘s Elements (Proposition 1 and Proposition 2) around 300 BC, but was probably known before this.

The algorithm builds upon Properties 1 and 4 from above. The value of $n$ in Property 4 is chosen to be $n=-\lfloor v/u \rfloor$ which leads to the equality $\text{gcd}(u,v) = \text{gcd}(u, v \text{ mod } u)$.

The algorithm can be implemented quite concisely in C++, one way of doing it being the following:

  template <typename NUM>
  NUM gcd_euclid(NUM u, NUM v)
  {
    while (true) {
      if (!v) return u;
      u %= v;
      if (!u) return v;
      v %= u;
    }
  }

Note that this implementation is almost identical to the Boost implementation, which, however, checks for zero-valued variables by comparing to an actual zero-object instead of relying on an object-to-bool conversion.

This generic implementation works for both built-in integer C++ types and number objects such as natural_number from the Kanooth Numbers library.

Note that every time u %= v is executed we have $u \leftarrow r$ where $u = q v + r$ and $0 \leq r < v$ behind the scenes. With the exception of the very first time this statement executes (where we may have $u < v$) we have $q \geq 1$. This implies

$$u = q v + r \geq v + r > 2r,$$

which in turn means that the value of $u$ at least halves every time u %= v is executed. Of course, a similar statement holds for v %= u. This shows that Euclid's algorithm computes a remainder (roughly) at most $\log_2 u + \log_2 v$ times. For a thorough analysis see Section 4.5.3 of The Art of Computer Programming, Volume 2, by Donald E. Knuth.

Two interesting things about Euclid's algorithm should be noted. First, the analysis of Euclid's algorithm is intimately tied to continued fractions (update 2009-11-10: See also Continued Fractions and Continuants). Second, the input numbers that make the algorithm perform the most remainder-computations are two consecutive Fibonacci numbers—supposedly the first practical application of the Fibonacci sequence.

Stein's Algorithm

Another way to compute the greatest common divisor was published by Josef Stein in 1967. It builds upon Properties 4 (with $n=-1$), 5, and 6 and thus only relies on subtraction, division by two and checking whether a number is even. Since division by two and odd/even checking are especially attractive on binary computers, the algorithm is also known as the binary gcd algorithm.

A possible implementation is this:

  template <typename NUM>
  NUM gcd_stein(NUM u, NUM v)
  {
    if (!u) return v;
    if (!v) return u;
    unsigned s = std::min(shift_to_uneven(u), shift_to_uneven(v));
    while (u != v) {
      if (u > v) {
        u -= v;
        shift_to_uneven(u);
      } else {
        v -= u;
        shift_to_uneven(v);
      }
    }
    return u <<= s;
  }

Since the algorithm itself only works for positive numbers, the first two lines take care of the cases where one input number is zero. Next, the value of $u_2$ is determined (the number of 2-factors, in the notation introduced earlier) and at the same time setting $u \leftarrow u/2^{u_2}$ (which is what shift_to_uneven(u) does). Similarly $v_2$ is determined, setting $v \leftarrow v/2^{v_2}$, and then finally $s \leftarrow \min(u_2,v_2)$. Assuming for the moment that the while-loop puts the greatest common divisor of two odd numbers into $u$, the algorithm finishes by returning $2^s u$. We have thus used the equality $\text{gcd}(u,v) = 2^{\min(u_2,v_2)} \text{gcd}(u/2^{u_2},v/2^{v_2})$.

We now focus on the while-loop. Note that the first time the loop is entered both $u$ and $v$ are odd. Now assume $u$ is larger than $v$. The algorithm sets $u \leftarrow u - v$ which makes $u$ even, and then repeatedly divides $u$ by $2$ until $u$ is odd. (If $u$ had been smaller than $v$ the same operations would have been performed with $u$ and $v$ interchanged.) We now see that at the beginning of each while-loop iteration, both $u$ and $v$ are odd.

It is clear that each iteration of the while-loop makes the larger of $u$ and $v$ strictly smaller. So at one point either $u$ or $v$ becomes zero and we can use Property 1 to terminate. But it is convenient to stop just before this happens and since only even numbers are divided by two, this can only occur through a subtraction. And a subtraction can only result in zero if the two quantities involved are equal. This explains the termination criteria for the while-loop.

The shift_to_uneven function could have the following implementation.

  template <typename NUM>
  inline unsigned shift_to_uneven(NUM& n)
  {
    unsigned shift = 0;
    while (!(n & 1u)) {
      n >>= 1;
      ++shift;
    }
    return shift;
  }

Some remarks are in order with regard to efficiency. Every time shift_to_uneven is executed inside the while-loop we know that the number is even, so the initial check !(n & 1u) is superfluous. Similarly the return value of shift_to_uneven is not used inside the while-loop, but it should be fairly easy for the compiler to observe this.

Finally, if working with multiple-precision numbers, the binary shift operation can be expensive compared to a (constant-time) test-bit method, which tests whether a certain bit is set. Given a test-bit method, zero bits could be counted, starting from the least-significant bit, followed by a single binary shift operation. Both Kanooth Numbers and GMP has such a test-bit method, but the code naturally becomes less generic.

How many times is the while-loop executed, in the worst case? Either $u$ or $v$ is reduced by at least a factor two, so, similar to Euclid's algorithm, the loop is executed at most $\log_2 u + \log_2 v$ times.

It should be noted that Alex Stepanov has written some notes that, among many other things, deal with generic implementations of both Euclid's and Stein's gcd algorithms (see Section 10.2). Stepanov has also written the book Elements of Programming with Paul McJones, which presents a mathematical approach to programming. The book also mentions Euclid's and Stein's algorithms, but the treatment in the notes is more comprehensive.

Running Time Comparisons

This section presents some results from comparing the Euclid and Stein algorithms for computing the greatest common divisor. All tests were run on a 2.5 GHz AMD Phenom 9850 Quad-Core, running 64 bit Mepis Linux and using a GCC 4.2.4 compiler.

Built-in integer C++ types

The following experiment was done.

1. Create an array (of length, say, 2000) of random numbers, uniformly distributed from 1 to the largest representable value.
2. Compute the gcd of the first and second number, the second and third number, the third and fourth, and so on, until all numbers from the array have been used. Add together all the gcd-results (for some simple algorithm validation and to avoid unwanted compiler optimizations).
3. Perform Step 2 a fixed number of times (so a second or so passes).

Steps 2 and 3 were timed using different gcd algorithms (but using the same array of numbers): The Euclid and Stein algorithms from this article, an optimized Stein's algorithm, and the Euclid and Stein algorithms from Boost.

The results can be summarized as follows.

• The implementation of Euclid's algorithm presented in this article and the gcd_euclidean version from Boost performed virtually identically.
• This article's implementation of Stein's algorithm could be optimized a little, but the effects were no more than around 3%.
• For 32 and 64 bit unsigned integers, Stein's algorithm was faster than Euclid's by 12% and 37%, respectively.
• For 8 and 16 bit unsigned integers, Euclid's algorithm was faster than Stein's by around 13% (I am not sure why these smaller word sizes changed the faster algorithm).
• The gcd_binary version of Stein's algorithm from Boost performed worst of all for all built-in data types, around 70-75% slower than the Stein's algorithm from this article.

The Kanooth Numbers Library

A number of files were created. One with 100 random numbers consisting of 1-2000 bits, with the bit length also chosen at random. Another file with numbers consisting of 1-4000 bits, and so on, thereby ending up with several files where the average bit size for each file were around 1000, 2000, 4000, 8000, 12000, and so on.

The procedure was then the same as for the built-in types, see steps 2 and 3 from the previous section. Similarly, Euclid's and Stein's algorithm from this article and from Boost were used, along with an optimized version of Stein's algorithm (using a test-bit method as mentioned earlier).

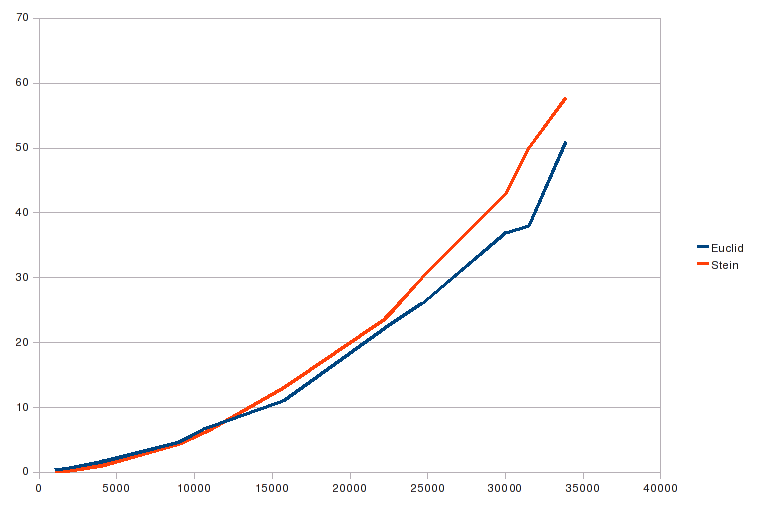
The results are illustrated in Figure 1, where only Euclid's and the optimized Stein's algorithm are depicted. The following comments regard the test algorithms not shown.

• The two versions of Euclid's algorithm were indistinguishable.
• The generic Stein's algorithm from this article was indistinguishable from the Boost version.
• The generic Stein's algorithm was consistently around 32% slower than the optimized version.

As can be seen in the figure, Euclid's algorithm was faster than Stein's from an average of around 12000 bits or more.

Note that although Boost's version of Stein's algorithm was relatively slow for the built-in integer types, here there was no difference compared to the generic Stein's algorithm. This is most likely due to the fact that the majority of the time for multiple-precision arithmetic is spent doing the actual arithmetic operations, where the Boost algorithm's indirect indexing was too slow compared to the fast processor arithmetic. Strangely, Boost defaults to using the binary Stein's algorithm for built-in unsigned types and Euclid's algorithm otherwise. A resonable choice, but their Stein's algorithm could use some rewriting.

The GMP Library

The same test method and data files as the Kanooth Numbers test were used, and GMP equivalents of this article's Euclid and optimized Stein algorithms were tested. The results can be seen in Figure 2. This time, Euclid's algorithm was faster than Stein's for all number sizes.

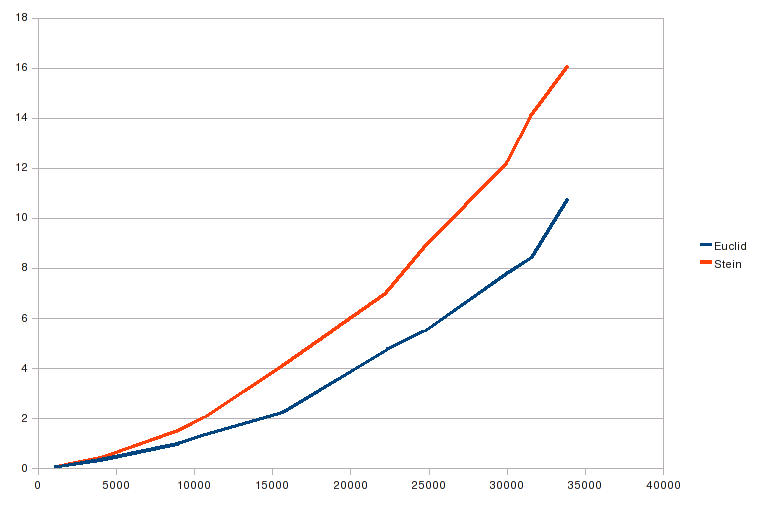
Although this article is by no means a Kanooth Numbers versus GMP face-off, a comparison can rightly be made. The exact same input data and equivalent algorithms were used. For Euclid's algorithm, the GMP algorithm was consistently 4.5-5.0 times faster. The same was the case for Stein's algorithm, although the running times approached each other as the bit size of the input numbers went down.

One more algorithm was tested, by the way, and that was GMP's own gcd algorithm. The results were not shown in the figure, however, because they were (as good as) identical to the results of the Stein algorithm. According to the GMP manual, the binary Stein's algorithm is in fact used. For large input numbers, however, GMP's own gcd function apparently switches to another method. The same page also states that the “binary algorithm has so far been found to be faster than the Euclidean algorithm everywhere.” Well, not everywhere.

Conclusion

The purpose of this article was to present and compare two common algorithms for computing the greatest common divisor of two integers: Euclid's and Stein's (binary) algorithm. Both algorithms work well, and only a constant factor will usually distinguish them, if implemented properly.

On the basis of the results presented in this article, the following can be said. If the input numbers fit into the processor's natural word size, Stein's algorithm was faster than Euclid's. For multiple-precision numbers, Euclid's algorithm was faster than Stein's. This immediately suggests a hybrid method: Use Euclid's algorithm until the involved numbers fit into a register each, and then use Stein's algorithm to finish. Such a hybrid method becomes less generic, however.

If I had to choose a single all-purpose gcd algorithm, it would be Euclid's. It is simple to implement and it generally performs very well.

The running time results are not conclusive. Implementations details and testing methods can always be discussed but most importantly: Different hardware setups should be tried (and perhaps different compilers). If anyone is interested, I can make the test programs available for download.

(Update 2014-03-25: Source code for Euclid's and Stein's algorithm are available at GitHub as gcd_euclid.hpp and gcd_stein.hpp.)